初探系統動力學和延遲
每當住進飯店,洗澡時水龍頭都要調好幾秒,才能達到合適的溫度,手稍微往熱水一扳,就被燙得哇哇叫,調回來又覺得太冷。
儘管我們知道慢慢調整水溫是最好的,但它背後的原理是什麼呢?開始討論前,我們要先了解「系統」。
初探系統
「系統」這個詞被用在許多場合,例如電腦有「作業系統」,汽車有「動力系統」,學測要考「物理系統」,我們身在一個「社會系統」,甚至人體也是一個系統。但是,系統到底是什麼?
籠統地說,系統可表示為「事物間的關係與作用」,例如你手拿著 1kg 的物品,由於重力和正向力抵銷,物體靜止不動,這就是一個手、物體和地面組成的系統。當然,系統不單解釋實際物理狀態,也探求經濟、社會變化等議題。
系統由三個要素組成:元素、關係和功能,例如人體中的紅血球,就是血液循環系統的元素,而紅血球與各細胞交換物質、心臟推動血液的速度就是它們的關係,而功能就是我們關注的目標,看你怎麼定,研究「如何達到血液最高流速」也是可以的。
一般來說,元素被替換對系統不會造成太大影響,人的血液細胞每三個月換一次,我們還是活得好好的。而關係和功能就相當重要,若哪天紅血球不運送氧氣,人類就滅亡了。
元素間的關係包括「正回饋」和「負回饋」,例如「收入 -> 利潤」是正回饋,收入越多利潤越大,而「支出 -> 利潤」是負回饋,它們增減是反向的。

多個回饋合起來,便可形成「迴路」。
晚睡導致晚起,晚起又導致晚睡,這是「增強迴路」。
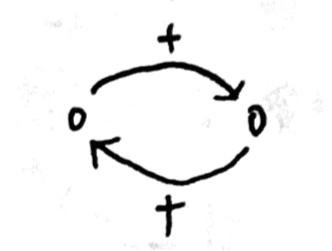
獵物多導致掠食者多,掠食者多導致獵物少,兩者處在一個平衡狀態,這是「調節迴路」。
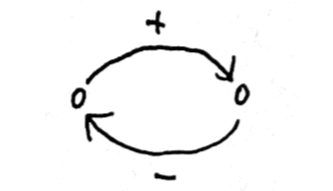
分析複雜迴路,我們可以探求事物間的關係。
水龍頭系統
(這裡我用《系統之美》的畫法,左邊流入右邊流出,兩者都有控制閥門)
當前水溫和預期溫度組成溫差,溫差決定調熱水的幅度(這邊假設冷水固定,也就是溫度流失速率固定)。
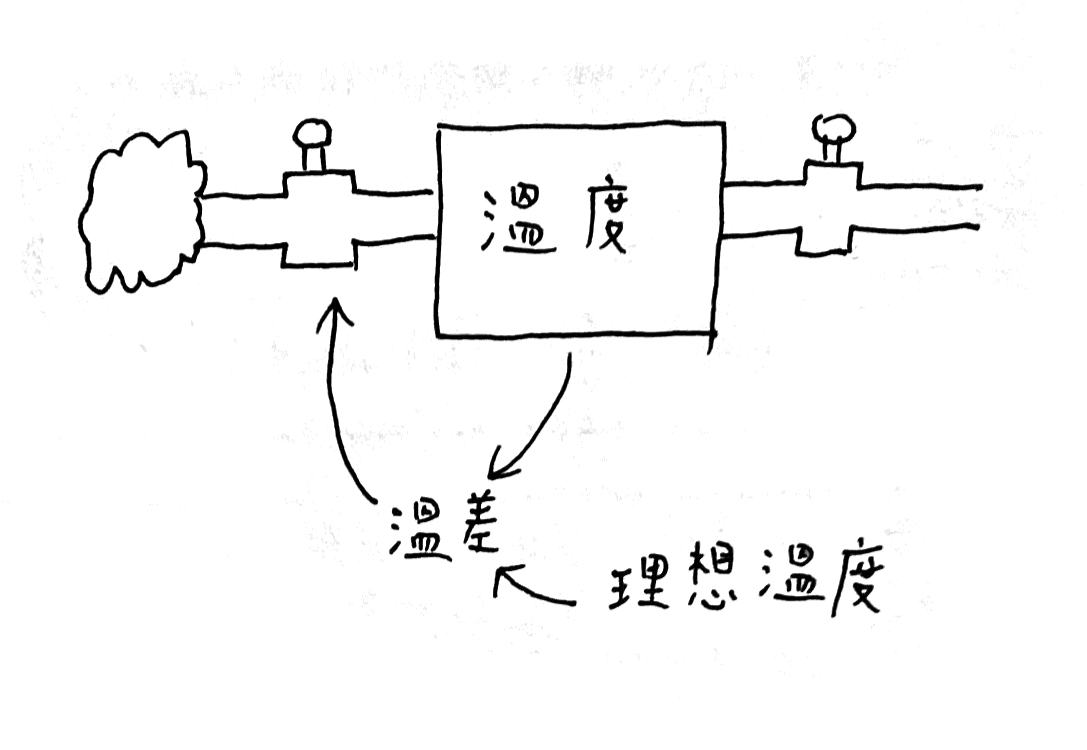
假設水溫調節和溫差關係如下:
: 水溫 : 時間 : 調水溫的幅度 : 當前溫度 : 理想溫度
解微分方程:
由於
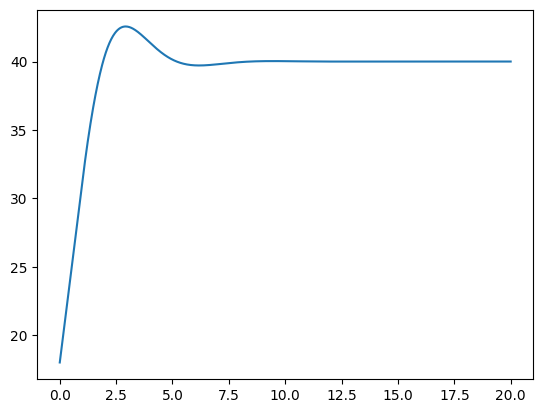
圖形長這樣:
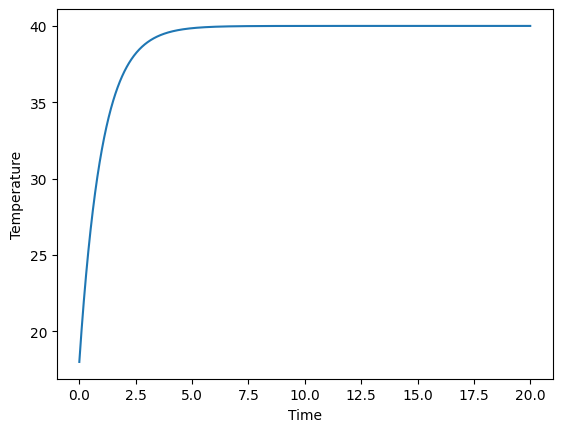
看起來溫度不會上下震盪?
在這個例子,我們假設調節幅度即時反應到溫度,實際上,熱水要過一段時間才能送達,因此式子要改。
: 水溫 : 時間 : 調水溫的幅度 : 當前溫度 : 理想溫度 : 熱水延遲時間
當下調整水龍頭,要經過 d 秒才能作用,因此 t 秒時斜率取決於 t-d 秒的溫度。
一段一段算延遲微分方程,對於
對於
算到後來,得出所有
假設
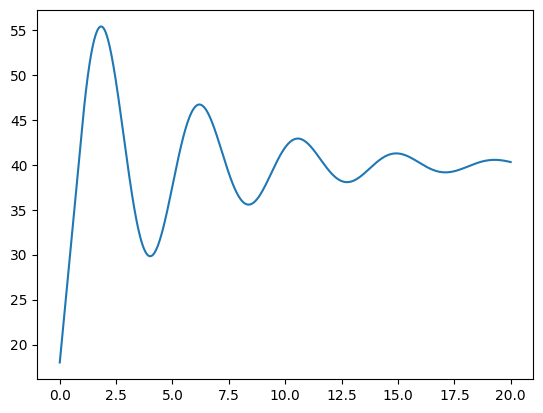
若
由此可知,在
這也適用在許多方面,例如股票市場、存貨管理,若公司管理者向上游廠商下單時,過於依靠短期銷售量,而忽略長期趨勢和不確定因素,便會導致存貨過多或不足。
對於個人也是如此,很多時候我們看到一則新消息,注意力忍不住被吸過去。過個幾天,又忘記之前看了什麼,真正重要的目標反而被落下。
在充滿延遲的複雜系統中,慢一點反而更好。